We are all tired of the pandemic. We’d like to wake up one day and have life returned to normal. A big step towards normalcy would be allowing schools to open in the fall. Schools provide education, social environments, and meals to their students. Schools also provide a chance for parents to have free time for work or relaxation. However, schools are an optimal place for the virus to spread: a daily mass gathering. Following John Harte’s great piece on mass gatherings, we would like to discuss important considerations for reopening schools, and what to look for over the next couple of months to better understand the risks.
Key uncertainties still exist in thinking about school reopenings. For example, we don’t fully know the role that children and young adults play in amplifying transmission, and early reports have suggested they might be both less susceptible to the virus and less infectious—with the strong caveat that, in many cases, schools were closed when these studies were conducted. We thus do not have much information about the rate at which the virus spreads in the school setting. Understanding how rearranging chairs, requiring masks, staggering classes, and other precautionary measures can reduce transmission will be key to safe reopenings in the fall. However, school-reopening risk depends both on these factors that modulate transmission potential within the school, as well as on the probability of someone coming to school infected.
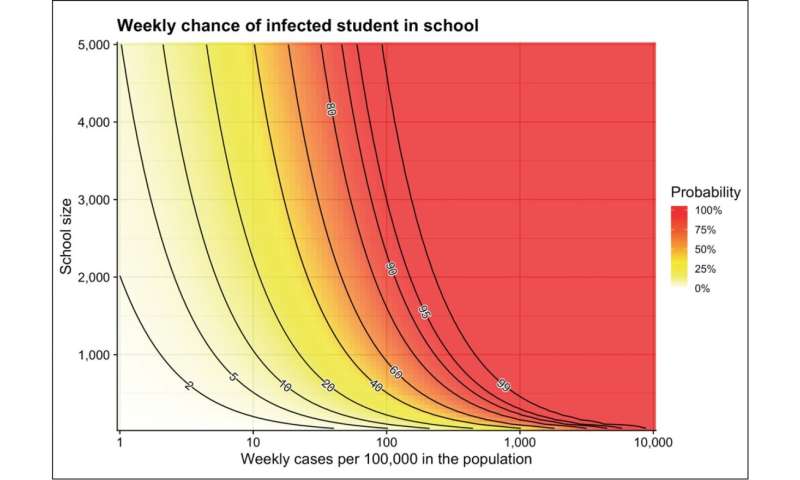
Thus, we would like to ask the simple question: What is the chance that, in a given week, one of the students comes to school infected with the virus? This chance will depend on two things: (1) the chance that a student gets infected over the week, and (2) the size of the school.
We first look at the chance of infection. Austin, Texas, for example, is currently (July 2020) seeing around 300 new reported cases a day, which is around 2,000 a week, in a population of 2 million. Not accounting for underreporting, the average person in Austin therefore had a one in 1,000 chance of getting infected last week.
As an example, let us use this number, one in 1,000, as the chance for infection of each student. A group of 10 students in Austin will have roughly a one percent (10/1000 or one in 100) chance that one of them becomes infected in a week, and the chance becomes roughly 10 percent (100/1000 or one in 10) for a group of 100 students. Multiplying the number of students by the chance is, of course, only an approximation. A school with 2,000 students does not have a chance of 200 percent to have an infection! Though in this school of 2,000 students, there will be on average two infected students coming in every week. To calculate this chance exactly, we reframe the question to first ask about the chance that not a single student gets infected. The probability for a student to not get infected is 999 in 1000—a high chance. That event has to happen 2,000 times in a school of 2,000 students, giving a chance of 999/1000 to the power of 2,000, which is 14 percent (or about 1/e2). Thus the chance that at least one student gets infected is 86 percent. Every week, the school has an 86 percent chance that an infected student will come to study in class.
Using this simple math, we get the graph above, which shows us, as calculated before, that in a school with 2,000 kids and a weekly infection rate of 100 in 100,000—like the current general rate in Austin—there is about an 85 percent weekly chance a student gets infected. If this infection rate was lowered to 10 in 100,000 (roughly the current rate in the UK), then the chance drops to 20 percent, whereas if we halved the school size to 1,000 students it drops to 60 percent, and to 40 percent for 500 students. It’s clear that both of these factors can drastically alter a school’s risks in the fall. We also see that dividing a school in two has a larger effect when the infection rate is lower. For example, halving the school size can decrease the weekly risk from 85 percent to 60 percent, from 99 percent to 90 percent, and from 99.9 percent to 97 percent. But when the rate is lower, risk is approximately halved. We go from 20 percent to 10.5 percent and from 10 percent to 5.1 percent. Though the average chance for an outbreak is not halved, the average number of outbreaks is; of course, the maximum size of each outbreak would also be halved.
There are many complexities we haven’t considered here. It is clear that not everyone in a community will have the same chance of getting infected—essential workers and lower socioeconomic groups and their families may be at higher infection risk, because they can’t fully isolate at home. Preventative measures like checking for fever and other symptoms could also reduce the risk, though this will likely be leaky given the high proportion of transmission occurring before or in the absence of symptoms. Widespread testing for the presence of the RNA of the virus could reduce the risk further, by not relying on symptoms.
Source: Read Full Article